학습목표

마코프 체인의 성질을 이해할 수 있고, 고정적 상태를 구하는 방법에 대해서 고민해본다.

홱심 키워드

• 마코프 체인(Markov Chain )
• 상태(state)
• stationarity
• 고정된 분포(stationary distribution)
• irreducible/reducible
• 재귀 상태(recurrent state)
• 과도적 상태(transient state)
• 무방향 네트워크(undirected network)에서의 Random walk

학습하기

학습내용

마코프 체인

• 마코프 체인은 어떤 상태에서든 다른 상태로 가는 것이 가능(확률 > 0)할 때 irreducible하다고 한다.

(→ 'from anywhere to anywhere') 

• 어떤 상태에서 시작해서 그 상태로 (언젠가) 돌아오는 확률이 1일 때, 그 상태를 재귀 상태(recurrent state)라고 한다.

 $(\leftrightarrow$ 반대 개념은 과도적 상태transient state)

• 상태의 수가 유한한 irreducible한 마코프 체인은 모든 상태가 재귀적이다.

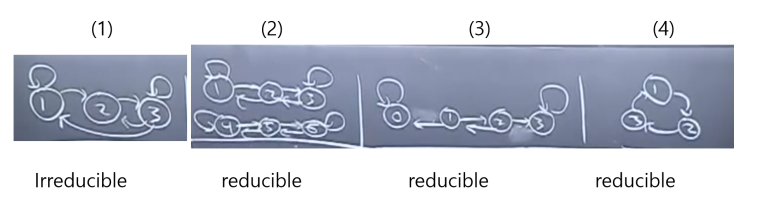
(1)은 irreducible 하며, 유한한 상태가 있기 때문에 각 상태는 재귀적recurrent할 것이다.

(2)는 reducible 하지만, 1-2-3과 4-5-6 각각을 irreducible 한 체인으로 쪼개서 볼 수 있다. 

또한 만약 1-2-3과 4-5-6을 잇는 모서리를 만들어서, 1-2-3을 돌다 4-5-6으로 넘어가버리는 체인을 만든다면, 각 상태는 과도적(transient)이 된다(원래 시작했던 상태로 돌아갓 루 없으므로)

(3)에서는 0이나 3으로 가 버리면 영원히 그 상태에 머물게 되므로, 0과 3을 흡수상태(absorbing state)라고 하며, 이 체인은 도박꾼의 파산문제(Gambler's Ruin)를 마코프 체인 형태로 표현한 것과 같다.

(4)는 반복적인(repetitive) 마코프 체인이라고 부른다.

Stationarity

정의) 확률벡터  \vec s  ​s​⃗​​ 는  \vec s Q = \vec s  ​s​⃗​​Q=​s​⃗​​ 를 만족할 때 고정적(stationary)인 상태라고 한다.

정리) reducible 하고 유한한 갯수의 재귀적 사태를 가진 마코프 체인은

1. 고정적인 상태  \vec s  ​s​⃗​​ 가 항상 존재한다.
2. 고정적 상태  \vec s  ​s​⃗​​ 는 유일하게 존재함(unique)
3.  s_i = \dfrac {1}{r_i}  s​i​​=​r​i​​​ ​1​​ 를 만족시키는 r_i  r​i​​ 가 존재한다. (r_i  r​i​​는 $i$ 에서 시작했을 때, $i$ 로 돌아가는 데까지 걸리는 시간이다)
4. 어떤 $m$ 값에 대하여  Q^m  Q​m​​ 의 구성 성분이 모두 양의 값을 가질 때, 

  $n\to \infty$ 함에 따라 P(X_n= i) \rightarrow s_i   P(X​n​​=i)→s​i​​ 한다.

 $\iff$ 모든 확률벡터  \vec t  ​t​⃗​​ 에 대하여  \vec t Q^n \rightarrow \vec s  ​t​⃗​​Q​n​​→​s​⃗​​ 를 만족한다. 

가역 마코프 체인(Reversible Markov Chain)

정의) 전이행렬  Q = (q_{ij})  Q=(q​ij​​) 를 가진 마코프 체인은 모든 상태 i, j에 대하여 

 s_i q_{ij} = s_jq_{ji}  s​i​​q​ij​​=s​j​​q​ji​​ 를 만족할 때 가역적(reversible)하다고 한다. 

정리)  \vec s  ​s​⃗​​ 에 대하여 가역적일 때,  \vec s  ​s​⃗​​ 는 고정적이다.  

증명) 모든 i, j에 대하여  s_i q_{ij} = s_jq_{ji}  s​i​​q​ij​​=s​j​​q​ji​​ 를 만족할 때, 

 \displaystyle \sum _i s_i q_{ij} = \sum _i s_j q_{ji} = s_j \sum _i q_{ji} = s_j  ​i​∑​​s​i​​q​ij​​=​i​∑​​s​j​​q​ji​​=s​j​​​i​∑​​q​ji​​=s​j​​

따라서,  \vec s Q = \vec s  ​s​⃗​​Q=​s​⃗​​ 이 성립한다.  

 d_i  d​i​​가  $i$의 degree(딸려있는 모서리 수) 라고 했을 때 (그림에서는 d_1 = 2, \space d_2= 2, \space d_3= 3,\space d_4= 1)  d​1​​=2, d​2​​=2, d​3​​=3, d​4​​=1), 

모든 i, j에 대하여 d_i q_{ij} = d_j q_{ji}  d​i​​q​ij​​=d​j​​q​ji​​ 를 만족한다. 

증명) $i\ne j$ 라 했을 때,  q_{ij}, \space q_{ji}  q​ij​​, q​ji​​는 둘 다 0이거나 둘 다 0이 아니다.

모서리 $\{i,j\}$가 존재할 때,  q_{ij} = \dfrac{1}{d_i}  q​ij​​=​d​i​​​ ​1​​ 이고, 따라서

 $1,2,...,M$ 의 꼭짓점들과  degree  d_i  d​i​​ 가 있을 때,  \vec s = \dfrac{d_i}{\sum _j d_j}  ​s​⃗​​=​∑​j​​d​j​​​ ​d​i​​​​ 인 \vec s  ​s​⃗​​ 는 고정적이다(stationary).